Do They Really "Get It?" {3 Ways to Check During Math Class}

Has this ever happened to you?

You teach a lesson, let's say, about adding fractions. As you're walking around the classroom, lots of kids have correct answers - even a few that you wouldn't expect. You're patting yourself on the back and decide to give them a problem that's just a little bit harder. (At this point, I always think to myself, "They've GOT this! We are FLYING through this lesson!")

After a few minutes, you realize: they don't really know what they're doing yet, and you wonder what happened just a few moments ago.

Over the years, this has happened to me so many times that I wondered if there was even a way to really know if they "get" a concept before they crash and burn and I want to cry.

Here are some ideas I've tried to see if kids are really "getting it" in math class:

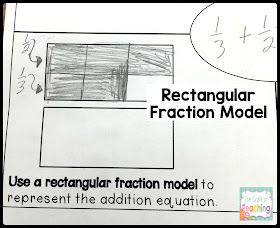
1. Can they draw a picture or make a model?

Even in fifth grade, the power of visualizing a math problem is, well...powerful! With younger students, I encourage the students to draw exactly what they see when a problem is presented. With older students, I teach them how to use models to represent the parts of the problem they are working on. (Sometimes, they still draw the actual picture, and I think that's ok too. I just try to get them working towards something that won't take quite as much time!)

If they are having trouble drawing a picture or creating a model or representation, that tells me a lot about how they are processing the problem.

You can see this adding fractions product by clicking here.

2. Can they write a word problem?

This is ALWAYS eye opening for me. I can usually tell right away how students are understanding a problem or equation by how they write their word problems. (I can also tell if they can actually visualize the problem from their number story!)

First, we have to define how to write one - this is key!

Once the students know what a word problem looks like and sounds like, I can start to see understanding through their stories. This mainly helps me assess whether they know how to properly apply their knowledge of different operations. It's fairly evident that they aren't sure what subtraction really means if the story problem written will result in an addition situation!

This student was writing a word problem for 1/2 + 1/3.

When I read his problem, I could see he understood that he was combining the two fractions since he used the word "altogether." He also uses an object that can easily be split up into fractions, telling me that he has some understanding of what fractions actually are! (Not to mention he uses cupcakes - which makes his teacher very happy!)

Writing word problems is one of my favorite ways to see if students truly have an understanding of the type of problem they are trying to solve.

3. Can they clearly explain it to someone else?

We've all been there, right? You are obviously explaining something in the clearest way possible and the person you are talking to is looking at you with an expression of utter confusion. And this happens to students all. the. time. They think they are being clear, but the person listening has no idea what they are talking about. (This includes me sometimes!) In the upper grades, I think getting feedback and reflecting on their work is essential to learning how to be clear and concise with their mathematical explanations. Besides being clear with their speaking, they also have to learn how to be clear and concise in their written explanations.

One way we accomplish this is by using museum walks to provide feedback to each other and reflect on our own work.

Each team completes their own work on a poster, then we hang them up and use sticky notes to provide comments and questions about the work on the posters. Each team gets their own poster back and uses the comments and questions to revise their thinking or make their explanation more clear. This has worked wonders for my students! Through this process they often find small mistakes (and big ones) and it helps them to see what others see when they look at their work.

It gives me insight into two things:
1. Can students look at others' work critically in order to provide useful feedback?
2. Can students use constructive feedback to revise their work?

I know this has been a hit in my classroom, because now they demand request time to get feedback on everything from their math work to their science notebooks! And I can see that they are becoming more clear in explaining and showing how they got their answers.

Click here to see the adding fractions product used throughout this post in my store.

__________________________________

Sometimes, it can be really tough to know if kids are really "getting it." I have used these ideas to help me gather information about my students for several years and I have learned more about them and their mathematical ideas as a result! It really helps me to inform my teaching - or possibly reteaching depending on what I find out. How do you assess your students to find out if they are "getting it" during math? I would love to hear from you in the comments.

Like this post and want to share? Click the red circle to pin it!